第15話　渡辺慧『認識とパタン』を読み解く ❖ 理系書探訪【書評記事】

◉ 1956年、IBMワトソン研究所に活躍の舞台を移した理論物理学者、渡辺慧は、近代厳密自然科学の方法論による “自由意志の謎”の解明に向けて、独自の情報理論の構築を開始します。本書『認識とパタン』は，1939年、情報論的エントロピーを世界に先駆けて導入した渡辺が、1960年代当時、情報理論応用の最先端課題 “パターン認識” に潜む深い意味を、平明な文章と実例で語ったもので、本件に関する唯一の一般向け解説書です。情報科学の記念碑的著作、『認識とパタン』探訪の旅にでかけましょう。

1．渡辺慧『認識とパタン』、“言葉” の本質、“直観” の謎に迫るパターン認識の伝説的古典

寺田寅彦の「物理学と生命科学／精神科学」統合の夢、生涯をかけてそれを探求した弟子、渡辺慧が世に送る “パターン認識” に関する一般向け解説書、

を取り上げます。本書刊行の2年後、同じく岩波新書の1冊に加わった、渡辺慧『生命と自由』については、当サイトの記事

をご覧下さい。

＊＊

かつては、小さな新刊書店でもみかけた本書。残念ながら、国立国会図書館デジタルコレクションの個人送信サービス・未登録本のようです。公共図書館を利用しましょう。図書館本の検索サイト「カーリル」は、ありがたい存在ですが、まだまだ、精度が低いようです。私、探訪堂の居住地を指定すると、『認識とパタン』は５館所蔵と出力されますが、公共図書館横断検索サイト「ゆにかねっと」経由では18館所蔵と出力されます。Amazonの古書販売では、現在（2025.06.16）、エディション「認識とパタン（1978年）」では、送料込み501円（本体1円）程度で入手できますが、新たなエディション「認識とパタン（岩波新書 黄版 36）」が追加されて送料込みで最低価格が2,500円程度となっていて、通常、こちらが優先表示されるようです。メルカリで個人が安値販売すると直ちに「sold out」タグがつき、Amazon等の古書販売に流れるという流れが定まりつつあるようです。

渡辺は、紙面節約のためか、 “パターン” ではなく「パタン」という語を使っていますが、本稿では、今風に “パターン” という語でいきます（引用文は除きます）。

1-1　渡辺慧『認識とパタン』、執筆の背景を知る

夏目漱石の門人でもあった寺田寅彦（1878-1935）は「日常身辺の物理学（寺田物理学）」の推進者として知られます。この寺田物理学、日本製家電製品などの深化の背景に、今も生き続けます（他国が真似できないはずです）。寺田本人の研究としては、漱石の句「落ちざまに虻を伏せたる椿かな」に端を発する椿の落下に関する研究などが有名ですね（註１）。

（註１）〝On the motion od a peculiar type of body falling through air —— Camellia Flower〟（『寺田寅彦全集 科學編　第五巻』の No.177：NDLDC ＊写真が本文の後に2ページ分、綴じ込まれています）

その一方で、物理学と生命科学の間に橋をかけること（未完に終わった『物理学序説（リンク： 国立国会図書館デジタルコレクション個人送信サービス）』など）を夢見ていました。たとえば、自由意志の問題について、つぎの言葉を残しています。

人間の自由意志と称するものは、有限少数な要素の決定的古典的な物理的機功では説明される見込みのないものであるが、非常に多数な要素から成り立つ統計的偶然的体系によって説明される可能性はあるであろう （寺田寅彦「蒸発皿」、1933年6月）

寅彦の立場は、たとえ自由意志の謎が解ける日がきたとしても、「科学はやはり不思議を殺すものではなく、不思議を生み出す」というものです。

“自由意志と統計力学” といえば、“自由意志とエントロピー” でしょう。時間の矢も関係してきます。エルヴィン・シュレーディンガー（1887-1961）の『生命とは何か（1944年）』に先立つこと、約10年です。フランスの哲学者アンリ・ベルクソン（1859-1941）や、同じ寺田寅彦の高弟、藤原咲平（1884-1950）も同様の趣旨の議論を残しています（渡辺慧『生命と自由』、第二、第三章）。

本書『認識とパタン』の著者、寺田寅彦門下の渡辺慧（1910-1993）が渡仏したのは1933年のこと、パリ・ソルボンヌ大学のルイ・ド・ブロイのもとでエントロピーと量子力学的な時間の向きの探求を開始します。1935年の学位論文「熱力学の第二法則と波動力学」でエントロピー概念の一般化を果たした渡辺慧でしたが、ドイツ・ライプツィヒのヴェルナー・ハイゼンベルク（1901-1976）のもとに移った1939年には、論文

• 熱力学の概念を原子核の標準状態に適用することについて
  （Über die Anwendung thermodynamische Begriffe auf den Normalzustand des Atomkerns、Zeitschrift für Physik Vol.113、1939、pp.482-513）

において、明確に「情報論的エントロピー」の概念導入に至ります（ハイゼンベルクの影響は甚大で、最晩年の渡辺は、物質と精神の問題、「心身問題」への相補性原理の適用を考えていたようです）。

さて、本題。
ルネ・デカルトを祖とする近代厳密自然科学が成立して以降、自然現象に「目的」という概念を持ち込むことは厳禁となり、ニュートン・ラプラスの決定性原理を基本とする因果的説明のみが許されることになります。それに対して、渡辺は、このフランス留学時代を振り返った論説のなかで、

因果性は、自然現象の、過去から未来への自動的発展を追う立場に結びついている。それに対して目的性は、未来において実現すべき目的をもった意志が現在に作用する立場に結びついている。この両者の一方から他方への移り行きは、それゆえ、或る意味で、時間の逆転に結びついている （渡辺慧「ベルグソンの創造的進化と時間」、1947（註2））

と述べています。渡辺慧にとっての “パターン認識” とは、因果論的秩序（自動的秩序）に支配された物質世界と、目的論的秩序（意志の秩序）のなかに存在すると渡辺が確信する精神世界との境界に存在する事象なのです。

感覚器官から脳に伝達された「情報」は、その変換に際し “観測” という量子力学プロセスによってエントロピーの瞬時的増大を招く。一方、生み出された情報は、その脳内での処理過程において、如何なる「統計力学的な」変化を引き起こすのか？ 「時間の探求」に区切りをつけ、米国IBMの研究所に移った渡辺慧は、パターン認識に着目、本書『認識とパタン』においても取り扱われる “醜い家鴨の仔定理” などを生み出していくのです。この定理、何と、認知する側に「何らかの意図」を仮定しなければパターン認識は成立しない、という結論に結びつき、“自由意志の謎の解明” に一歩近づくことになるのですが、、、。

（註2）渡辺慧の論説「ベルグソンの創造的進化と時間」は、『サンス フランス學術研究 第二冊（1947／11）』に掲載されたもので、そののち、渡辺慧『時』、河出書房新社（1974）などに再録されていましたが、この河出書房版は、渡辺慧『時間』、白日書院（1948）の再版です。元の白日書院版は戦後の紙の供給事情によって赤茶けた状態ながら、国立国会図書館デジタルコレクションの個人送信サービスにて閲覧できます。

1-2　渡辺慧『認識とパタン』、言葉，パターン、パターン認識

本書、第Ⅰ章「パタンとパタン認識」は、目の前の机を見て「私は机を見る」というとき、それは「私の見ているものを机と見なす」ことである、という説明から始まります。「見る」と「見なす」の違いはゲシュタルト心理学の “二義性のある図形” がはっきり教えてくれるといいます。本書に掲載されている図は有名な「あひる兎」と「盃／二婦人」ですが、ここでは、カニッツァ『視覚の文法』からつぎの図、《兎／二女性》を紹介しておきます。

コーレンの兎／二女性図形（1969）、
カニッツァ『視覚の文法：ゲシュタルト知覚論（NDLDC）』、p.163より

20世紀は「哲学的認識論」から「科学的認識論」に移行した時代とされています。哲学的認識論の議論で有名なものが、 “普遍論争（普遍者論争）” 。 神の存在証明に関係して古くからある議論のようで、〝犬一般〟や〝人一般〟や〝机一般〟を「普遍（普遍者）」といい、犬ならば〝ポチ〟や〝コロ〟や〝ジョン〟などを「個物」とよびます。そこで、隣の家で飼っているポチやコロは実在するが、「犬一般」などは存在しないといった議論が発生します。西洋中世では、神は個物か普遍者かという議論もありました。この話題は、本書の第Ⅲ章で本格的に説明されます。

さて、パターン認識の場合、「目の前にある机という個物を机と見なすこと」を、その個物にあるパターン（類似性）を認め、それを “机” という「類（分類、クラス）」に入れ込むこと、と理解します。この一連の過程を「パターン認識」といいます。そのために、「机をあと１脚ほしい」などと考えることが許されるわけです。なお、本文では、広範囲に渉る話題から具体例を取り上げて、丁寧な説明があります。

さて、個物の性質は機械に理解できる「データ」によって代表され記述されます。パターン認識が成立するためには、類を創造するという作業（クラスタリング；パターン認識の学習段階）と、既成の類を機械に教え実際に分類する作業（パターン再認識；パターン認識の分類段階）が必要です。概念の獲得と概念の伝達のための概念定義の方法には、外延法（実在する個物のデータから定義する方法）と内包法（類の必要十分条件を与える方法）があり、破綻をさけるために例外を認めないという意味で、数学的概念などでないかぎり、内包法の適用は不可能です。確かに、「机」という類の必要十分条件を例にとれば、その困難さが理解できます。一方、外延法では、無限の個物を与えることは不可能なため、実際には、外延でも内包でもない「範例（パラダイム）による学習」を採用するといいます。具体的には、親・教師役が「有限個の類の範例で示すこと」ですが、これは第Ⅳ章で議論されます。

1-3　渡辺慧『認識とパタン』、パターン認識において “データ” とは何か

本書の第Ⅱ章「データをどう取るか」の議論は、やや慎重に進みます。生なまのデータから個物を分類する、そのための “特徴づけデータ” を抽出するという議論ですね。渡辺慧は、欧州留学時代、生化学者の江上不二夫（1910-1982）、心理学者の宮城音弥（1908-2005）とも親交がありましたから、顔を合わせる度に、彼らと遠慮のない議論を行っていたと推測されます。本書の議論が、生化学や心理学のやや専門的な実例にも及ぶのは、そのような背景をもっていると理解したほうがよさそうです。個物からデータを取得するプロセスとして、視覚、聴覚だけでなく、臭覚や味覚なども考察範囲に加えてよいでしょう。

本書では、まず、「特徴づける」ことの定義を明確にします。それは、範例による分類を、内包（必要十分条件）による分類に近づけること、あるいはそのための変換であるとします。まず、「作為のない生のデータ」が必要となり、つぎに類似したものの集まりとしての類を生成することになりますが、全然、作為のないデータなど存在するのかという議論が本章のテーマ、そもそも「類似した」とは如何なることかについては次章で議論されます。

画像データでも音声データでも同じですが、これらのデータを振動数、振幅、位相のずれ方が異なる「波（正弦波）」の和に分解するという “フーリエ変換” を行うとデータの特徴付けには有効です。ところが、外界からの音を脳内信号に変換する感覚器官である「蝸牛かぎゅう管」の中では、管を通過する進行波の振動数ごとに反応する有毛細胞が異なるという事実が紹介されます（フォン・ベケシ（1899-1972）は本件でノーベル生理学・医学賞受賞）。つまり、人の聴覚情報処理においては、音の “フーリエ変換” に関連したデータこそ、脳が受け取る「生のデータ」であるというのです。

視覚データ処理では、背景と注目物を分ける必要があります。数学的には二階の偏導関数を使った「マッハ帯」と呼ばれる輪郭抽出法が知られていますが、多層で構成される視覚神経細胞の中には、なんと、微分演算をする一群の細胞が存在するというのです。これもフォン・ベケシの仕事です。そして、話しはいよいよクライマックス、「蛙の目は何を見るか」という議論に入ります。蛙の視神経は蛙自身の行動の範疇に密接に結びついていて、距離や反応速度、反応範囲などが、例えば食物である蚊などの捕捉に適合しています。

本章の結論として、機械が行なうパターン認識のための「データ」は、

(1)　目的に適った特殊性をもつ（データ量を減らすこと）
(2)　適当な普遍性をもとつ（蛙の目が、蚊しか認識できないのでは困る）
(3)　技術的経済的な最適性（高性能で安く）

が必要であるとして本章を締めくくります。

第Ⅲ章「類は実在するか」では、哲学における「普遍者論争」をとりあげ、そのなかで個物たちの「類似性」がどのように検討されたかを振り返ります。全てのデータの数値化が要求される科学的認識論では、個物たちの「類似性」はデータ間の “距離” で計ることになりますから、問題はその定義です。ところが、ここで、1961年の “醜い家鴨の仔定理” が登場するのです。つぎの表現では、パターン認識の対象に聴覚データなども含め、個物の替わりに “物件” とし、それを説明する特徴を “述語” とよんでいます。

ということは、醜いアヒルを加えたアヒルの仔たちをそれぞれに論理的に識別できるような仔細な特徴も含めて “述語” を列挙した場合、共通する述語数からはアヒルと醜いアヒルを区別できないという結論が導かれます。

この定理、「類似性は存在しない」ことを主張すると思いきや、ターゲットは別のところにあります。すなわち、“従来哲学が云う「認識」と「価値」は独立であるという主張” の誤りを指摘するものであって、それゆえ、物件データ間の距離という概念には、我々の価値観が反映されている必要があると結論づけるのです（具体的には述語に重み付けする）。私、探訪堂は、パターン認識の背後に存在するであろう “直感的判断” の存在を連想します（本稿、《2-1》参照）。そして、

普通のパタン認識の本は、この最も重要な点について何もいっていない　（渡辺慧『認識とパタン』、p.105）

と結びます。そういえば、自社AIの “教師なし学習” をアピールするウェブページなどで、外部からの “範例（パラダイム）” は使わず、また、内部に “評価指標” 相当のメカニズムも必要としないなどの説明を見かけることがあり、そんなとき「目がアヒル」になってしまうのは、私だけでしょうか（大企業の研究所の工学系研究者が作った高速移動体に関する超複雑な運動方程式の検討会に、物理系の研究者に混じって参加した経験があります。実験結果を次々に取り入れて補正につぐ補正を重ねて出来上がった精密で長大な方程式が、運動量保存則やエネルギー保存則を満足しないという結論に至って一堂、ビックリするのですが、このままでは動力源がなくても運動をいつまでも継続する可能性がある、、、。人工知能研究にも、物理系の保存則に相当する、厳守すべき原理原則が存在するのですね。渡辺慧が追求するのは、まさに人間の知的情報処理過程における原理原則なのです）。

1-4　渡辺慧『認識とパタン』、コンピュータ、パターン認識、そして人工知能へ

本書、後半の第Ⅳ章「コンピュータによるパタン認識」では、機械にパターン認識させるための数学的方法を、つづく第Ⅴ章「パタン認識と人工知能」では、機械が実行するパターン認識の出力の一意性の問題などが議論されます。ところどころ、数式が出てきますが、専門的な内容ではありません。ただし、本書の「はしがき」に、

一九七八年の秋には、パタン認識に関する国際学会が日本で開かれますので、それを良い機会として、パタン認識というものに関する一般の興味が高まることを希望しながらこれを書きます

と書かれているように、渡辺は、パターン認識の技術的細部には精通していています。この国際会議とのつきあいは長く、10年前の1968年には、在職していたハワイ大学のあるホノルルで開かれた会議の取りまとめのひとりに名を連ねていて、1969年に出版されたその議事録のエディターを務めています。

さて、本章の内容です。「類」を特徴づける有限個の特性（パラメータ）を軸とする空間において、物件はひとつの点として表されますが、その密度分布をクラスタリングに使うのが分布関数法です。さらに、極値法、類中心法などに話しが及びます。興味深いのは極値法に替わる「動力学的モデル」の話しです。これは実際に渡辺研究室で行われた課題と思われ、パラメータ空間での極値探索に微分方程式を使うというものです。極値問題の解法といえば、歴史的には物理学の課題解決を通して発展してきましたから、物理学者とすれば、ごく自然な発想です。

この第Ⅳ章で目を引くのは、渡辺流の情報エントロピーの話しです。代表作、渡辺慧『知識と推測』では、条件付き、相対、原因、結果、帰納などを冠したさまざまなエントロピーを定義し駆使して議論を進めていますが、本書『認識とパタン』では、データの凝集力とエントロピーを関連付けだけを紹介しています。「類（クラス）」の形成には、物件間の “類似性” だけでなく、“凝集力” とよぶべき特性も介在して、これで男と女、親と子、犬と猿といった類の近接性を説明できるとします。この凝集力は、集団の可能な状態の頻度の対数から求めた “情報エントロピー” の符号を反転した値として表現でき、実際に「寄宿舎の四人の女学生」という問題に当てはめて計算経過を説明しています。

各技術の話し、たとえば、パーセプトロンの説明は、

今では、この機械の成功は一つの数学の定理によるもので何も神経系統のまねというようなところにあるのではないということが明らかになりました （渡辺慧『認識とパタン』、p.136）

などと、簡潔かつ本質をついています。神経系を伝達する電気信号の挙動は動的なプロセスで、本来、微分差分方程式などで書かれるべきでしょうが、それを代数式に置き換えたところが偉大な点で、それまで、非ノイマン型のハードウエアを模索しつつ脳神経系の再現を目指していた人工知能研究は、一気に、従来機の内部での “プログラミング” の問題へと様相を変えるのです。

最終章、第Ⅴ章は、“帰納的推論としてのパターン認識” が主題です。

抽象化された大原則から、個々の事例の説明を引き出すのが「演繹的推論」、個々の事例を集めて大原則を導く過程が「帰納的推論」です。帰納的推論は結論が一意に決まらないという「多義性」をもちます。この多義性、“生命の自由” に関係した逆時間プロセス、逆因果性などを想起させます。その観点から、このクラスタリングの問題というのは “仮説創造” の過程であり、直感的かつ審美的な過程であり、それゆえ “価値体系” を背景にもつ価値判断を必要とします。機械（コンピュータ）に成し得るのは演繹的推論のみであり、直感的な価値判断を伴う帰納的推論は超理性的な知的飛躍であると念を踏みます。章の終わりでは、コンピュータと人間の脳の比較検討、いわゆる「脳のリバース・エンジニアリング」の現状が披露されて、解剖学・神経心理学的な知見から、人間の「前期哺乳類的頭脳」に相当する部分がなければ、真のパターン認識は不可能であるという結論を示します（半世紀ほど前の言葉です）。

簡単なようで奥深い本書『認識とパタン』。そもそも人工知能って何だろう、という疑問が湧いたら、ぜひ手に取りたい一冊です（本書が、早期に、国立国会図書館デジタルコレクション個人送信サービスで閲覧できるようになることを期待します）。

2．渡辺慧『認識とパタン』を読む、若干の蛇足

閑話休題。

2-1　形容詞を使わない名詞の世界

AIによる分類というのはありがたいものですが、しばしば、我々の理解と言葉を軽々と超えてきます。

それに関連して例示を求められたときにする話しがあります。たとえば、英語には兄と弟をひと言で表す単語がないのは何故という疑問です。大変なのは台湾の方と結婚した場合の話しで、たとえば、息子の娘、娘の娘や、さらには、息子の妻の最年少の弟などをひと言で表す単語が存在して、一説によると100種類を超えるとのことです。

それを遥かに超える話しは、アラビア語圏におけるラクダの名称だそうです。最も一般的な呼称は “イビル” だそうですが、状況によって異なる呼称をもちます。ラクダはとても大切な相棒だということでしょう。

言語の歴史の研究者から、人類の言語の発達においては名詞が先で形容詞は後、という話しを聞いた覚えがあり、上のラクダの話しもそのとき伺いました。機械によるパターン認識では、人の理解を超えるクラスターが形成されて、各クラスターを分離して表現する適当な形容詞がみつからないということがありますが、アラブのラクダの話しは参考になります。

教師なし学習の結果、数千、数万次元のパラメータ空間内において、互いに隣接はするものの、それらを分離する超平面で隔てられたクラスターたちは、言葉になる以前の「違和感」の現れであるはずです。それを、機械自身が、人の言葉に翻訳してくれる日は訪れるのでしょうか？ それとも、われわれは置き去りにされるのか？

2-2　AI を使わないパターン認識の話し（ここにだけ数式登場）

パターン認識の前準備には、個々の存在や現象の類似点を抽出する「データマイニング」、個々の存在や現象の類型を創造する「クラスタリング」があるわけですが、本書『認識とパタン』でも紹介されている例に、1968年から日本で実用化されている “郵便番号” があります。非常に巧妙なやり方で、「サイバネティックスの日本上陸」にも関連した動向です。ぜひ、調べてみてください。

私、探訪堂が係わった話しを少しだけ紹介しましょう。当時は “AI爆発” のはるか前でしたから、問題状況に応じて「郵便番号自動読取機」流のやりかたで個別的な解決を図る方法が普通でした。問題は、2次元図形の輪郭線が与えられたとき、それが何であるかを言い当てるというものです。

ひとつの閉じた曲線に限定して、これらの図形を認識するために、陰関数カーブフィットという手法を使います。数式が出てきて恐縮ですが、横軸 \(x\)、縦軸 \(y\) の関数として \(f(x,y)=0 \) という式で表現する方法です。半径 \(1\) の円は \(x^2+y^2-1=0\) と表現できます。これは2次の陰関数の例となっています。たとえば、4次の陰関数の一般形は \(a_{00}\;, a_{01}\;, a_{10}\;,... , a_{40}\) をパラメータ（助変数）とする式、

\( a_{40}\; x^4+a_{31}\; x^3y +a_{22}\; x^2y^2+a_{13}\; xy^3 \)
\( +a_{04}\; y^4+a_{30}\; x^3+a_{21}\: x^2y^2+a_{12}\; xy^2 \)
\( +a_{03}\; y^3+a_{20}\; x^2+a_{11}\; xy+a_{02}\; y^2 \)
\( +a_{10}\; x+a_{01}\; y-a_{00}=0 \)

です。まず、与えられた図形の重心を求め、重心からの平均距離や最大距離を求めて「標準サイズ」にそろえておきます。つぎに重心周りの回転モーメントという量を計算して、「主軸方向」を求めて向きを揃えます（上の右図の矢印）。こうした前準備を経て、いよいよ陰関数の当てはめを行なうのですが、そのためには「最適化」という手法で解いていきます。陰関数の次数 \(n\) を大きくすれば、一致度が増します。

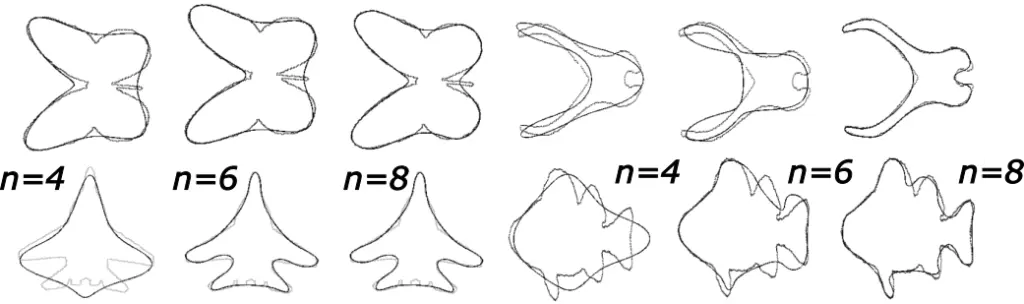
ところが、やり過ぎるとオーバーフィッティング（過学習）という現象が発生して閉曲線という条件が満たされないという結果が得られます（一部のデータ区間での一致度は抜群ですが、、、）。

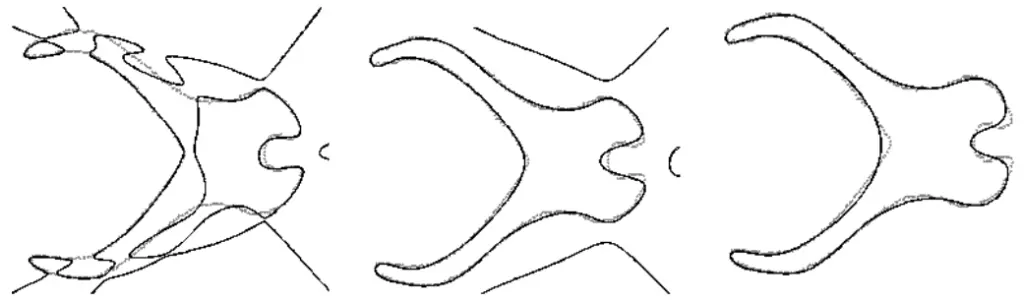
こうして、様々なデータから陰関数カーブフィットの結果としてのパラメータが決定されます。4次ならば、パラメータの空間は15次元、6次ならば28次元、8次元ならば45次元、、、14次ならば120次元などとなります。このパラメータ空間のなかでデータ点の塊（クラスタ）が重なりあっていなけれは、教師あり学習は成功で、そうでなければ、カーブの次数を上げて再挑戦です。

ニューラルネットワークを使ったパターン認識でも、この過学習という現象はエンジニアを悩ませる問題です。根本的に手順を組立て直さないと回避できない深刻な問題になることもあります（なお、上の例解は、私が参照した論文からの引用で、私自身の例題はその発展問題として説明困難なものです）。

3．《インターネットで読む》＊ 渡辺慧『知識と推測』、人工知能の根源に近代厳密自然科学で挑む科学的認識論の大作

本稿のタイトル本『認識とパタン』の背景にある渡辺慧、後期前半の大作

• Satosi Watanabe『Knowing and Guessing, A quantitative study of inference and information』、John Wiley Y Sons（1969）

の翻訳『知識と推測』です。原著の邦訳版は 1975年に4分冊、1987年に2分冊として東京図書から出版されました。再刊された2巻本は、国立国会図書館デジタルコレクションの個人送信サービスで読むことができます。

上巻冒頭、「驚き」が対数関数を使って定義され “驚きの加法性” が示されて「期待される驚き」から “無知” が定義されます。そして、“情報 = 無知の減少” と定めて、その後の長い議論がスタートします。ページが数式で埋め尽くされていきます。知識を定める命題の集合を考えて、各命題の有限個の論理和（“または”で結ばれた命題）や論理積（“かつ” で結ばれた命題）などの論理演算（ブール代数）で新しく生成される命題群をすべて取り込んで、それを数学的構造をもつ集合、「束（ラティス）」として把握します。忍耐が必要です。

上巻の山場は、 “演繹と観察” に統計力学はボルツマンのH定理とブリルアン流の精密なネゲントロピー概念を導入した議論と、本稿タイトル本『認識とパタン』でも登場した “帰納と学習” に対する「逆H定理」の議論です。

下巻は、“論理と確率” に関する深い考察から始まります。「遡見的確率は、そこに登場する二つの命題によって決定できない」ということの証明を見据えています。醜い家鴨の仔定理の原型が証明されます。

『認識とパタン』で示されたものとは、雰囲気が違います。

“論理” は演繹的推論であり因果論的秩序（自動的秩序）に支配される。一方の “確率” は帰納的推論であり目的論的秩序（意志の秩序）に関係するといったことが想起されます。左脳と右脳ですね。渡辺慧が、論理による人工知能構築を夢見る「第5世代コンピュータ」の動向に背を向けたのは、こういう根拠に基づいていたのですね。

つづく “クラスと概念” に関する考察では、クラスタリングのアルゴリズムが分析されます。、「非ブール的情報理論」の枠組みが示されて、量子物理学との関係が考察されます。ブール束に現れる分配法則を緩めた形で定義した「モジュラー束」上で確率論と情報理論を再構築するという試みですが、なんと、量子力学に関連してバーコフやフォン・ノイマンが研究したモジュラー論理との一致を見ます。渡辺慧婦人、渡辺ドロテアの研究対象でもある仏典に頻繁に登場する文言，「AはBにあらず、Bにあらざるにあらず」は解けるのか？ 捩り鉢巻きが必須です。

4．《インターネットで読む》＊ ミンスキー・パパート『パーセプトロン』

米国人工知能界の超大御所、マービン・ミンスキー（1927-2016）とシーモア・パパート（1928-2016）の共著『パーセプトロン： パターン認識理論への道』です。パーセプトロンの理論的限界を示した本書が契機になって、つぎつぎとスポンサーが撤退して、人工知能研究が10年にもおよぶ「暗黒時代」に突入するという「いわく付き」の一冊です。凝りに凝った図が多用されて、それを見るだけで楽しいのですが、パーセプトロンの全てが詰まってます。

5．《インターネットで読む》＊ アイゼルマン他『パターン認識と学習制御』

崩壊前のソ連邦が生んだ “ルネサンス人”、マーク K. アイゼルマン、パターン認識の大家、エマヌエル・ブラヴェルマン、ポントリャーギンの最適制御理論を変分学的見地から再構築した非線形制御論のレフ・ロゾノエルが、パターン認識のために開発した「ポテンシャル関数法」解説する教科書です。

数式沢山の本格的専門書で、巻頭まえがきは、訳者を代表してあの北川敏男が担当しています。アイゼルマンを「この方面の世界的権威」とよんでいます。パターン認識の議論を幾何学化するという方針のもとで、複雑なパターンの認識の問題から教師なし学習までを網羅しています。

6．ヤン ルカン『ディープラーニング 学習する機械』、畳み込みニューラルネットワークの創始者が語る

フランスの偉大な研究者にして、人工知能研究を「暗黒時代」から救い出したディープラーニングの父、ヤン・ルカン（1960-）がAI革命とディープラーニングの過去現在未来を縦横に語る、世界的ベストセラー。いずれ、当サイトで読み解いてみたい1冊です。

7．岡谷貴之『深層学習 改訂第2版』、深層学習の各種手法の意義、構造、応用を俯瞰する

ディープラーニングの教科書は数多いのですが、各種技術の羅列に終始して、その技術がどのような事態で効果を発揮するのか、なかなか理解できない場合があります。本書は、具体的なコード（大抵はPython）こそ示されていませんが、数式のコード化に困難を感じないエンジニアのバイブルになり得る教科書です。第3版が楽しみな1冊です。