◉ 現代数学の中心概念のひとつ、“多様体” は非線形科学の数学的舞台であり、曲線や曲面の概念を一般の次元に拡張/抽象化して得られる。多様体上の各点では、それを基点とするベクトル空間を考えることができ、それらを束ねてベクトルバンドルという “多様体” ができあがる。各点に滑らかに従属する正値対称行列を対応させると計量テンソルを定めたことになり、多様体上で測地線の解析ができる。今回は、先輩に「M を多様体、T(TM) を接バンドルの接バンドルとして、、、」などと言われて目を丸くしている新人さんのために、可微分多様体論の代表的な教科書2冊を中心にとりあげて紹介しよう。
改訂第2版 準備中
2024.04.21 公開
1.多様体論(微分可能多様体論)について
▼ 服部晶夫『多様体 増補版』、岩波全書(1989)
▼ 志賀浩二『多様体論』、岩波基礎数学選書(1990)
章を追う毎に、つぎからつぎへと新しい概念が組み込まれて、混乱が深まって行く。しかし、慣れてしまえば手放せない舞台装置となります。この明るく巨大な装置を離れると、人々との意思疎通が困難な “けもの道” に分け入ることになります。そんな数学世界の高速道路網、多様体論の世界にようこそ。
この導入部では、いきなり細部に立ち入るのを避けて、私、探訪堂の拙い概説から始めることにしましょう。取り扱う “多様体” は微分可能多様体(可微分多様体)と呼ばれるクラスです。もっと原始的な研究対象として位相多様体とかホモロジー多様体などもあり、こちらはトポロジー(位相幾何学)の話しです。
1-1 多様体の定義と接バンドル
素朴な曲面概念を 「多様体」 に一般化する手順は、
- 基礎位相空間とよぶ独立変数が作る集合を考え、座標を定めた開部分集合で各点を覆ったうえで、重複部分では他方への座標変換を定めておく
である。“位相空間” は、各点が所属する開集合を定めた集合、“空間” は、ある種の構造を与えた集合のことである。“素朴な曲面概念” は、曲面の「陰関数表現」や「パラメータ表現」から始める解析幾何学の曲面理解をいう。逆に、与えられた陰関数表現やパラメータ表現が、抽象化された多様体を定めているかは、それらの表現のヤコビ行列の階数で判定できる(陰関数定理等)。多様体論では “多様体でありさえすれば成立する” 結果に着目する。具体的な「図形」としての差異を見るためにはベクトルバンドルや遠くは分類空間などの概念が必要となる。2次元の多様体の代表例に、平面、球面、トーラス面(一人乗り浮き輪の表面)などがある。周期的に変化するひとつの変数とひとつの実変数を独立変数とする関数や微分方程式を扱いたければ、考察の舞台とする “多様体” を、数直線を母線とする円筒面にとればよい。
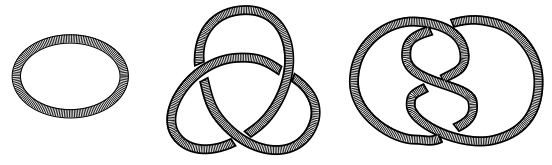
図は、ドーナツ型の図形(トーラス面)の3次元空間における実現の例。多様体論ではこれらを区別せず、これらに共通する幾何学的性質に関心をもつ。
1-2 多様体上の微分方程式と接バンドル
多様体の各点には、多様体と同じ次元をもつベクトル空間を付随させることができて、これを各点における接空間とよぶ。この接空間を多様体のすべての点にわたって束ねると接バンドルという概念を得る(バンドルは “束” を意味する)。各点でひとつのベクトルを選択し、これが多様体上で “連続的に” 変化するならば、これを多様体上のベクトル場(要するに連立常微分方程式系)という。ベクトル場は接バンドルの “断面” として幾何学的に把握できる。すなわち、多様体上の連立常微分方程式系を “幾何学的な図形” として解析できて、微分位相幾何学の手法が使えたりするのである。多様体論の凄い点、つまり初心者に優しくないところは、多様体上のベクトル場を “1階の準線形連立偏微分方程式系” と考えることである。その完全積分可能条件として登場するラグランジュ括弧式やポアソン括弧式が多様体上のリー群論や葉層構造論、ファイバーバンドルの理論へと繋がる。
1-3 多様体概念の展開
多様体上に定めた開集合の重なりにおける座標変換は、接バンドルを一般次元化した多様体上の “ベクトルバンドル” に対し、離れた2点での同一次元のベクトル空間の間に同型写像を誘導する。その写像は正則行列で表現できるから、一般線形群の元である。そこで、ベクトルバンドルにこのような群の作用を入れ込めば、ファイバーバンドルという概念が得られて、許容される “断面” の様相をより具体的に特定できる。この概念は、群の作用(対称性)を考慮した微分方程式の解析にも役立つ(リー群論)。また、二つのベクトルの内積の定義を場所ごとに連続的に変化させる “計量テンソル” を定めれば、一般相対論の舞台となるリーマン多様体の概念を得る。さらに、多様体の各点に有限マクローリン展開の係数が作る “アファイン空間” を割り当てるとジェットバンドルという概念を得るが、これを使うと多様体上の連立偏微分方程式系が “幾何学化” されて、代数的位相幾何学の手法のひとつである “コホモロジー” を活用して積分可能性を解析できたりする。
こんな具合に、つぎからつぎへと新しい概念が投入され、各概念が深化しつつ融合されていくのである。先輩は大喜びだが、新人は大混乱かつ大迷惑。ところが、これらの議論をどこまで進めようとも、そもそもの出発点である各開部分集合での座標設定に依存しないという点が重要。この性質を “コーディネート・フリー” (座標系非依存)という。“多様体の定義” が少し面倒な理由は、この性質を保証するためだったのである。また、様々な状況において、得られた結果が局所座標の取り方に依存しないことを保証する必要にも迫られるのだ。
2.多様体論の文献
2-1 邦文文献
微分可能性を考慮しない用語に “位相多様体、ホモロジー多様体” があるが、一般に、“多様体” といえば可微分多様体(微分可能多様体)を意味するそうなので、ここでもその意味で使う。私の時代の代表的な教科書はつぎの3点である。
- 松島与三『多様体入門』、裳華房数学選書5(1965)
- 服部晶夫『多様体 増補版』、岩波全書(1989)
- 志賀浩二『多様体論』、岩波基礎数学選書(1990)
松島与三(1921 - 1983)の『多様体入門』はこの分野の古典。英訳本もある。日本語版はその邦訳といった様子で、英語版のほうが違和感なく読めた記憶がある。志賀の『多様体論』は、岩波講座基礎数学の第一次刊行本『多様体論 1-3』の3分冊(1976)を合本したもの、服部の旧版『多様体論』は1976年発行である。以下の「3 内容紹介」で取り上げるのは、“ベクトルバンドル” を含めている服部と志賀の教科書である。参考文献によく挙げている教科書だが、ある時,後輩から2冊とも入手困難です、などと苦情を言われて、ずいぶん驚いた記憶がある。両者、オンデマンド版で復活したようで、特に、『多様体論』は当時の3倍の価格が付いていて、さらに驚いた。そういえば、古本屋のご主人が、「専門書を買ってくれるのは大学院生だけですよ」と言っていたことを思い出す。
2-2 英文文献
上記3冊に対応する英文文献は何だろうと考えてみるのだが、なんといっても経験不足で語るべき材料がない。ここでは、数理科学の一学徒としての拙い経験から、独断と偏見で、つぎの3冊をあげておこう。
- Morris W. Hirsch『Differential Topology』、Springer(1976)
- Frank W. Warner『Foundations of Differentiable Manifolds and Lie Groups』、Springer(1983)
- Amiya Mukherjee『Differential Topology, second edition』、Birkhäuser(2015)
Morris W. Hirsch(モリス・ハーシュ;1933 -)は、定性的微分方程式論の有名な入門書、スメール、ハーシュ『力学系入門』の著者のひとり。他方のスティーブ・スメール(1930 -)は高次元ポアンカレ予想問題の解決者でフィールズ賞受賞者である。このハーシュ『Differential Topology』の後半は微分位相幾何学の話題で、高次元ポアンカレ予想問題を目指してモース理論からコボルディズム論へと向かう。
2冊目のFrank W. Warner(フランク・ワーナー;1938 -)は微分幾何の専門家。『Foundations of Differentiable Manifolds and Lie Groups』の前半は『多様体 増補版』や『多様体論』に対応する。Lie群と題した第3章は丁寧・簡潔で分かり易い(Lie群やLie環の教科書というと、どれも本格的すぎて重く、フーリエ級数論を群論の言葉で語るために既約ユニタリー表現などが登場する頃から脱落してしまうのだが、ワーナーの第3章は軽快である)。後半は層係数コホモロジーからホッジ理論に向かう。そういえば、服部『多様体 増補版』では、多様体の各点近傍で定義された可微分関数の全体はベクトル空間ではないが、“関数の芽”(開近傍の共通部分で一致する関数を同値として得られる同値類)として扱える、という注意書きがあった。
3冊目のAmiya Mukherjee(アミヤ・ムケルジー)の教科書は、ハーシュのテキストを分厚くしたうえで、丁寧に説明し直したという感じで、 “目から鱗” の記述にあふれている。目標は一般化ポアンカレ予想問題を解決に導いたスメールの定理の証明である。私、探訪堂は、上記2冊を古書で入手したが、Mukherjee は新刊本ながら格安のバーゲン品として入手できた(送料込みで4,000円ほど;ときどきこういう事があります)。
3.内容紹介
3-1 服部『多様体 増補版』
まず、服部『多様体 増補版』から見ていこう。著者、服部晶夫(1929 - 2013)は代数的位相幾何学の重鎮で平成元年度から日本数学会理事長を二期務めた。岩波基礎数学選書『位相幾何学』や『多様体のトポロジー』などの著作で知られる。『位相幾何学』は志賀の『多様体論』と同じ岩波基礎数学選書の1冊として合本された。これは全520ページの大作であり、最後の第13章は、志賀の『多様体論』最終章にも含まれる「分類空間」の話題に当てられている。
服部晶夫『多様体 増補版』、岩波全書 288、pp.283(1989)、B6判
序章 基礎事項の準備
集合/ベクトル空間/位相空間/微積分からの準備
第1章 多様体の概念
多様体の定義/ \( C^r \) 写像/ 1の分割
第2章 接ベクトル
接ベクトル空間/ \( C^r \) 写像の微分/ 接ベクトルバンドル
第3章 ベクトルバンドルと多様体
ベクトルバンドル/多様体のはめ込みと埋め込み.部分多様体/横断正則写像/付属バンドル/ベクトルバンドルの切断.リーマン計量と向き/第1、2、3章 問題
第4章 ベクトル場と微分作用素
助変数群とベクトル場/リー微分/外微分
第5章 接続とリーマン計量
2階常微分方程式とexp写像/接続と平行移動/リーマン接続/第4、5章 問題
第6章 管状近傍と横断正則性定理
管状近傍/境界をもつ多様体/横断正則性定理/第6章 問題
第7章 微分形式の積分
微分形式の積分/チェイン上の積分/第7章 問題
問題解答、あとがき、索引
本書は簡潔な記述ながら多くの実例説明がある。ときおり挟み込まれる《注意》書きは本書の範囲を超える話題への良き案内となっている。各章ごとの《問題》も教育的配慮に富む。なお、本書にあって、志賀『多様体論』にない話題に、2階の常微分方程式系の表現に関連したスプレイの概念がある。
3-2 志賀『多様体論』
つぎに、志賀『多様体論』をみて見よう。著者、志賀浩二(1930 - 2024)は微分位相幾何学の研究者で、ジョン・ミルナー(1931 -)の『モース理論』の翻訳書や本書『多様体論』のほか、『無限からの光芒: ポーランド学派の数学者たち』、『数学30講シリーズ』全10巻、『[対話]20世紀数学の飛翔』全5巻、『数学が生まれる物語』全6冊、『数学が育ってゆく物語』全6冊、『大人のための数学』全7巻など、多くの著書がある。残念なことに 2024年2月に逝去された。訳本『モース理論』の巻末には「訳者による付録 I 可微分多様体の基礎概念」pp.171-188 が添えられていてる。
志賀浩二『多様体論』、岩波基礎数学選書、pp.377(1990)、A5判
序章 多様体論の成立
座標をもつ空間/曲線と曲面概念の拡張/多様体の誕生/多様体の実現/多様体の類/接ベクトルと接バンドル/複素多様体の定義
第1章 多様体の基礎概念
多様体の定義/基礎的な諸結果/多様体の例/Whiteney位相/ \( C^0 \) 多様体から \( C^\omega \) 多様体まで
第2章 ベクトル・バンドル
ベクトル・バンドルの一般論/普遍ベクトルバンドル/滑らかなベクトル・バンドル/計量/はり合わせと \( GL(p; \mathrm{K}) \) 主バンドル
第3章 多様体上のベクトル・バンドル
接バンドル/ベクトル場のLie環と葉層構造/余接バンドルと微分形式/テンソル場とLie微分/体積バンドルと積分/Lie群とLie環/ジェット・バンドル/微分作用素
第4章 接続
接続の基本概念/曲率と平行移動/Riemann計量から導かれる接続/正規座標/法バンドルと管状近傍
第5章 ファイバー・バンドル
主バンドルと同伴バンドル/ファイバー・バンドルの一般論/等質空間/枠バンドル/被覆多様体
第6章 de Rham コホモロジー
de Rham コホモロジーとČechコホモロジー/de Rham の定理の証明/曲率とPontrjagin類
第7章 多様体論の展開
Sardの定理と一般の位置/分類空間/楕円型複体
解答・ヒント/索引
本書は各章ごとに山場がある。ときどき現れる細字の解説文には、毎回、唸らされる。なお、章末の問題は険しいものが多い。たとえば、第1章の章末問題、冒頭の1には「長い半直線」とか「長い直線」が登場する(これらは最小の非可算全順序集合を添え字集合とした単位半開区間のコピーの族を “密着” させてとった和集合)。これらの概念の定義は、当時入手可能な邦文教科書になく、
- James Munkres『Topology second edition』、Prentice Hall(2000)
などに当たる必要があった(このMunkresの本、第1部は位相空間論、第2部は代数的トポロジー。腹の底から理解できます)。
なお、本書、第6章の de Rham コホモロジーとČechコホモロジーの取り扱いは、概念形成を重ねながら、一歩一歩登ってゆくスタイルで、まことに分かり易い。これに対し、同じ内容を扱う、
- Warner『Foundations of Differentiable Manifolds and Lie Groups』、Springer(1983)
の第5章は、層係数コホモロジーの定義から始まる(層の話しというと3歩も4歩も引いてしまうが、この概念に対するWarner流の語り口は明快)。なお、コホモロジーは関数(一般には微分形式) \( \omega \) の微分 \( d\omega \) を求めるという演算の繰り返しから定まる “複体” を経て得られる代数的概念、一方、領域 \( R \) の境界 \( \partial R \) を取るという演算の繰り返しからはホモロジーがでる。これらの概念は一般化されたストークスの定理(初等的には重積分と3重積分を等式で結ぶ公式)で関連づけられる。
4.検討
解析的な教科書や代数的な教科書に慣れた読者にとって、現代数学の大系に連なり、異なる分野の様々な概念を取り込みながら巨大化するという特性をもった “多様体論” の専門書は、なかなかの難物である。初見の概念が説明なく現れれば思考が止まる。私は、『多様体論』を紐解きつつ、しかし、どうしてもわかった気になれないとき、該当する章ごとに、行間を他書を参照してノートに埋めつつ、別にプロジェクトペーパーを用意してペン書きで本文を写経した上で、さらにその上に鉛筆で注釈を加えるというアホな作業を繰り返した記憶がある。今や、そんな苦行は必要なく、下記に示すような “よい教科書” が容易に手に入る時代となった。
さて、これらの書籍を読み解く際の予備知識であるが、服部『多様体 増補版』はそれらを序章で要約している。高校数学にはない概念として、ベクトル空間のテンソル積、外積代数、位相空間論の初歩、微積分では陰関数定理や常微分方程式の解の存在と一意性の定理が含まれている。一方、志賀『多様体論』では必要とされる予備知識について明言を避けているようであるが、物語風に書かれた序章を読み終えることができれば大丈夫であろう。この序章では、2次元の多様体に限定したうえで、素朴は曲面概念から “多様体” をどのように定義するか(なんと、3種類の定義が試される)、抽象的に定義された多様体をどのように “実現”(十分大きな数空間のなかで表現)するか、微分するという概念と接ベクトルという概念の関係などが語られる。
4-1 松本幸夫『多様体の基礎』
『多様体 増補版』も『多様体論』も多様体の構造を入れ込む基礎位相空間をハウスドルフ空間(任意の異なる2点の近傍で、互いに共通部分をもたないものが存在する空間)としているが、実質的に第2可算公理を満たす “パラコンパクト空間(任意の開被覆が局所有限開被覆で細分される空間)” であることが求められる。この条件を欠くと、開被覆に従属する “1の分割” の存在が保証されず、たとえば、任意のベクトルバンドル上でリーマン計量が存在するなどの重要な結果が使えない。ところで、救いの神が降臨している。
松本幸夫『多様体の基礎』、東京大学出版会
は、線形代数と多変数関数の微積分の基礎知識のみを仮定している教科書で、位相空間については「開集合」から始めて第1章で「§5 位相空間」という節を設けて解説している。これで、多様体上の多重積分に関する「ストークスの定理」まで到達できる。なお、“1の分割” を導く際、パラコンパクト性ではなく、より分かり易い “σコンパクト性” を使うなど、初学者への配慮満載である。
松本幸夫『多様体の基礎』、東京大学出版会基礎数学5(1988)、pp.344
第1章 準備
多様体とは/\( m \) 次元数空間/ベクトル空間/連続写像と \( C^r \) 級写像/位相空間
第2章 \( C^r \) 級多様体と \( C^r \) 級写像
多様体の定義/\( C^s \) 級関数と \( C^s \) 級写像
第3章 接ベクトル空間
接ベクトル空間/\( C^r \) 級写像の微分/写像の局所的性質/射影空間
第4章 はめ込みと埋め込み
はめ込みと埋め込み/埋め込み定理/1の分割/正則点と臨界点
第5章 ベクトル場
ベクトル場/積分曲線
第6章 微分形式
1次微分形式/ \( k \) 次微分形式/外微分とストークスの定理
付録A \( D^r_p(M) \) と \( T_p(M) \) の関係
付録B 射影平面 \( P^2 \) が \( R^3 \) に埋め込めないことの証明
演習問題解答/参考文献/索引
4-2 松島与三『多様体入門』
往年の名著、松島与三『多様体入門』は5章構成、計58節、全282ページである。位相空間論の入門を少し外れる内容については、§14と§15でパラコンパクト性と1の分割(単位の分割)の詳細を説明している。この教科書、バンドルの概念こそ使わないものの、終始、解析的な取り扱いで登攀しつつ、中盤には早くもド・ラームコホモロジー群やド・ラームコホモロジー環の定義が姿を現し、最終節でストークスの定理の多様体上での証明に到達する。読み始めは、その独特のテンポに戸惑うものの、慣れれば使いやすく、何でも書いてあるので重宝してます。
松島与三『多様体入門』、裳華房数学選書5(1965)、pp.282
Ⅰ 序論
位相空間/ベクトル空間/ \( n \) 次元数空間\( R^n \) と \( C^r \) 級関数/逆関数の定理
Ⅱ 可微分多様体
多様体の定義/可微分多様体の例/可微分関数と局所座標系/付記.可微分構造の従属性と同値性/可微分写像/接ベクトルと接ベクトル空間,リーマン計量/関数の微分と臨界点/写像の微分/Sardの定理/リーマン多様体の運動/多様体の挿入と埋め込み,部分多様体/ベクトル場と微分作用素/ベクトル場と1パラメータ変換群/リーマン多様体の無限小運動/パラコンパクト多様体と単位の分割/多様体の位相に関する種々の注意/複素多様体/概複素構造
Ⅲ 微分形式とテンソル場
\( p \) 次線形形式/対称テンソルと交代テンソル,外積/付記.対称積と対称多元環/多様体上の共変テンソル場と微分形式/テンソル場のリイ微分と微分形式の外微分/写像による共変テンソル場の変換/多様体のコホモロジー環/複素多様体上の複素微分形式/微分式系と積分多様体/積分可能な概複素構造への応用/極大連結積分多様体
Ⅳ リイ群と等質空間
位相群/位相群の部分群と商空間/位相群の同型と準同型/位相群の連結成分/位相群の等質空間,局所コンパクト群/リイ群とリイ環/リイ群上の不変微分形式/1パラメーター部分群と指数写像/リイ群の例/リイ群の標準座標系/複素リイ群と複素リイ環/リイ群のリイ部分群/線形リイ群/リイ群の商空間および商群/リイ群の同型と準同型,リイ群の表現/連結可換リイ群の構造/1パラメーター部分群の微分可能性/局所コンパクト群がリイ群になるための条件/リイ変換群とリイ群の等質空間/等質空間の例
Ⅴ 微分形式の積分と応用
多様体の向きづけ/微分形式の積分/リイ群上の不変積分/不変積分の応用/ストークスの定理/写像度/ベクトル場の発散,ラプラシアン
あとがき/索引
5.国立国会図書館/個人送信サービスから
このコーナーでは、「国立国会図書館デジタルコレクション」の「個人送信サービス(無料)」を利用して、手元端末で閲覧可能な書籍を紹介します。下の各記事のバナー「国立国会図書館デジタルコレクション」からログイン画面に入ります。未登録の場合、そこから「個人の登録利用者」の本登録(国内限定)に進むことができます。詳細は当webサイトの記事「国立国会図書館の個人向けデジタル化資料送信サービスについて」をご覧下さい。
5-1 ケリー『位相空間論』
▼ ケリー『位相空間論』、吉岡書店数学叢書2,児玉之宏訳(1968)、pp.177
位相空間論の有名な教科書(専門書扱いで入門書をひととおり終えた人向き)に、
- John L. Kelley『General Topology』、van Nostrand(1955)
- Ryszard Engelking『General Topology』、Heldermann Verlag(1976、1988)
- Stephen Willard『General Topology』、Addison-Wesley(1970)、Dover(1998)
などがあります。これらの教科書、同じ用語でも定義や記法が微妙に異なることがあります。そのため、推論の帰結として得られる “定理” を流用する際は、抜けている条件を補うなどの「翻訳」が必要となったりします。Engelkingは癖が強く閉口しましたが、圧倒的な内容です。ところで、リストの先頭、ケリー(Kelley)の教科書は、この分野の用語や記号法の世界標準を作ったというような位置づけで、内容としても、ほぼ、何でも載っています。そして、この教科書の邦訳が、なんと、「国立国会図書館デジタルコレクション」の「個人送信サービス(無料)」で、手元端末にて閲覧できます。
5-2 鈴木治夫『微分多様体入門』
▼ 鈴木治夫『微分多様体入門』、サイエンス社(1979)
多様体論に関係した教科書で、オンラインで閲覧可能な教科書です。この教科書、第1章で直ちに “接ベクトル束” (接バンドル)の定義が現れますが、概念先行ではなく、松島『多様体入門』に近い、解析的な書き方です。そのため、手計算で行間を埋められます。多様体上のベクトル場から導かれる1階の連立偏微分方程式系の “解” の関連概念として、葉層構造論の話しが充実しています。最終章ではド・ラームコホモロジーから葉層構造の特性類、 “ゴドビロン-ベイ数” の議論に突撃します。
5-3 占部 実『微分方程式』
▼ 占部 実『微分方程式』、共立出版(1958)
多様体論やリー群論の成立背景を理解する上で、1階の準線形連立偏微分方程式系との具体的な格闘経験があると心強いと思います。1970年代頃までは、常微分方程式論のなかで、この項目が必ず取り上げられていたようです。ところが、最近の1階の偏微分方程式系に関する書籍は、逆に、多様体論をひととおり終えた研究者向けの高度で抽象的な話しになりがちです。ところが、私、探訪堂が、先輩諸氏から教えていただいたすばらしい教科書が、なんと、「国立国会図書館デジタルコレクション」の「個人送信サービス(無料)」で読めるのです。それが本書です。章末演習は証明問題ではなく計算問題でいっぱいです(例:次の連立偏微分方程式の一般解を求めよ。(1)〜(6)など、脳疲労の回復効果抜群)。第1部が「常微分方程式(8章構成)」、第2部が「偏微分方程式(5章構成)」です。第2部は1階の偏微分方程式限定です。全部で228ページ、分量的にはほぼ半々です。第1部第6章には連続変換群に対して不変な微分方程式の話題があり、リー群論や第2部の話しに繋がります。第2部では全微分方程式の話題もあります。“インボリューティブ・ディストリビューションが、、、” などと先輩に言われて途方に暮れているそこの「あなた」、ここに、その正体が書かれてますよ(言葉が大分違いますが)。ところで、本書、「微分方程式」でのNDL検索ではヒット数が多すぎて手に負えず、「占部」ではヒットなしでしたが、この共立出版、基礎数学講座の筆頭編集者名である「秋月康夫」でようやく見つけました。NDLのOCRには、向いていない装幀の本だったようです。私は古書で入手済みですが、NDLのデジタルコレクションの中に、やはり、あるんですね。「ビジョン2021-2025 国立国会図書館のデジタルシフト」に感謝です。
6.書斎の本棚/図書館の書棚から
このコーナーでは、本文に登場した本、関連書籍をさらに紹介します。
6-1 服部『多様体 増補版』
■ 服部晶夫『多様体 増補版』(岩波書店オンデマンド版)
現在、服部晶夫『多様体 増補版』は岩波書店のオンデマンド版として入手可能です(判型も同じ)。他書と違って、本書では、要所要所で圏論(カテゴリー論)の用語と解釈が述べられます。遠慮がちに
関手性は数学の現代的記述に非常にしばしば現れるものであるが、本書ではそれについての一般的な解説は行わない。しかしながら、本例をはじめ本書で扱ういくつかの例によってその性格は察せられるであろう。(服部晶夫『多様体 増補版』p.87)
などと書きつつも、その後もなお、関連する記述が顔を出します(p.118-9 に共変関手と反変関手が登場)。なお、岩波基礎数学選書の服部晶夫『位相幾何学』では圏論パワーが全開です。「圏論」の本格的な教科書は眩暈を引き起こしますから、まずは、この『位相幾何学』pp.7-11の要点解説や河田敬義『ホモロジー代数』(岩波基礎数学選書)の第4-6章あたりが無難かと思います。本書最終節では多様体に “特異単体” という構造を入れてチェイン上の積分を議論しますが、それに呼応するかのように『位相幾何学』の最終章は “CW複体” という構造を入れた空間上でのバンドルの議論です。そして、議論の中心はやはり、“ホモトピー関手” なのです。
6-2 志賀『多様体論』
■ 志賀浩二『多様体論』(岩波基礎数学選書 オンデマンド)
志賀浩二『多様体論』も、同じく、岩波書店のオンデマンド版で入手可能です。私はまだ、現物にお目にかかったことがありません。オンデマンド版と言えば、その昔、1990年代半ば頃だったか、チェック・ホモロジーを勉強する必要に迫られ、この分野の必読文献
S. Eilenberg『Foundations of Algebraic Topology』、Princeton Univ. Press(1952)
を購入したことがありました。UMI の Books on demand、今のオンデマンド版です。当時からあったんです。ケタ違いの価格で2万円を超えました。ところで、本書、本文でも吟味しましたが、志賀浩二の数ある著書の中でも、別格の存在感を放っています。
このようにして得られた接バンドルの概念は、実はもっと一般的な概念であるベクトル・バンドルの立場からみた方が、一層明解となる。(中略)多様体上の種々の概念または理論の多くは、単に接バンドルにとどまらず、多様体上の種々のベクトル・バンドルを用いて述べられ、展開されてゆくのが現状である。その意味で、ベクトル・バンドルの観点は多様体の一般論を見通しよく展望させる地点を与えているといってよいであろう。(志賀『多様体論』p.37)
こんな話しや、
多様体の研究を進めていくとき、問題によっては、多様体の枠にとどまらず、さらに新しい概念を導入し、多様体をいわば俯瞰するような立場を設定しておくことが望ましいことがある。そのような考え方を示す例として、ここでは分類空間の概念を説明しておこう。(志賀『多様体論』p.344)
などという案内が鏤められています。ヘルマン・ワイル『リーマン面』を彷彿とさせますね。
6-3 松島与三『多様体入門』
■ 松島与三『多様体入門(新装版)』(裳華房数学選書5)
本文でも紹介した松島与三『多様体入門』が、なんと、52年ぶりに本文組直し+レイアウト・デザイン刷新により、新装版として 2017 年に発売されています。書店でも確認しましたが、内容はそのまま、テンソル表現の上付き、下付き添え字の左右の位置関係等々、忠実かつ見やすく再現されています。位相幾何学と融合して、抽象度を増す一方の多様体論ですが、解析力学方面ではこの松島スタイルを踏襲している文献がたくさんあります。
6-4 松本幸夫『多様体の基礎』
■ 松本幸夫『多様体の基礎』(東京大学出版会)
本文でも紹介した松本幸夫『多様体の基礎』は増刷を重ねているようです。松本幸夫(1944 -)は微分位相幾何学や葉層構造論の権威、田村一郎(1926 - 1991)の研究室出身で、特に4次元多様体論では
上正明、松本幸夫『4次元多様体 Ⅰ、Ⅱ』(朝倉書店、2022)
など、多くの著書があります(この2冊本は図書館で借りましたが、超絶的、ここは諦めが肝心です)。1991年に発売された、松本幸夫『4次元のトポロジー』(日本評論社、B5判、ハードカバー)は表紙を変えながら引き継がれ、2016年には、ポアンカレ予想問題の解決を含めたインタビュー記事を加え、ソフトカバーの新版として再登場しました。本書『多様体の基礎』は、線形代数と微積分があれば、位相空間論の基礎などはひとつの節を当てて解説していますから、他書を参照しなくても読み進められます。この「第1章 準備」の内容を超えるような話しが登場した場合には、該当する節の終わりに、「§12の補足1 \(\alpha \) が無理数のとき、\( k_\alpha(\mathrm{R})\) が \( \mathrm{T}^2 \) の中で稠密なことの証明」とか「§12の補足2 ハウスドルフ空間の中の点列の収束」などとして解説しています。